The Humble-Nishiyama Randomness Game
What is The Humble-Nishiyama Randomness Game?
The Humble-Nishiyama Randomness Game is a game invented by two mathematicians: Steve Humble and Yutaka Nishiyama. It is a game that seems fair at the first glance, yet has a way to increase a chance of winning significantly.
The game is based on the idea of Penney Ante game in which 2 players select their own sequential outcomes (n = 3) of a coin toss (either HEADS or TAILS). The coin will be flipped repeatedly until one of the selected sequences comes first, and whose the sequence appears is the winner of the game. In the case of The Humble-Nishiyama Randomness Game, instead of using a coin, a deck of cards consisting 26 black cards and 26 red cards is used (either RED or BLACK).
The rule seems straight forward and fair. However, there is one great strategy that allows Player(B) has a bigger chance of winning than Player(A) up to 70%+
NOTE: Player(A) represents the first player who calls a sequence.
The Winning Strategy
Assume that Player(A) has selected a sequence RED RED BLACK. All Player(B) needs to do is that use his/her opponent sequence as a reference, take the second value, convert it into the opposite value, then put it in front of the sequence, finally ditch the last value.
Example Selecting RED RED BLACK
- Take the second value and convert it to the opposite RED -> BLACK
- Put the converted value in front of the sequence -> BLACK RED RED BLACK
- Finally ditch the last value -> BLACK RED RED
According to the table below, with this strategy, it is guaranteed that Player(B) will always have a higher chance against Player(A) whatsoever.
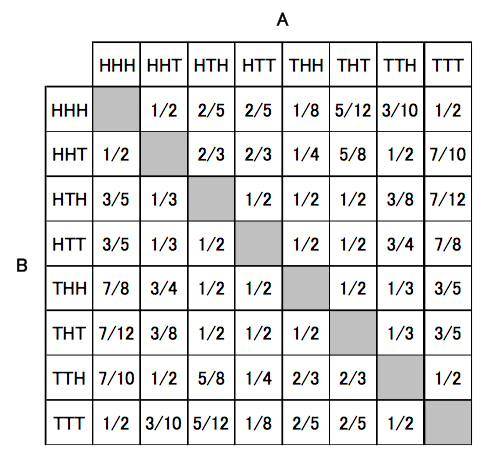
Experimental Procedures
The rules and the strategy are easy to understand, yet clearer evidence is still needed. Therefore, I decided to create a program that simulates the nature of the game. First, I created a GameEngine class that contains everything we need (e.g., deck, rules, algorithm, play, experiment).
- Create a GameEngine
# Import libraries
import random
from typing import List, Dict, Any
# Core Game Engine
class GameEngine:
""" Two players play the game using an ordinary deck of cards.
The cards will be dealt out in a row, one after another.
Before the dealing begins, each player claims an ordered sequence of colors that might turn up,
for example “red black red” (RBR) or “black red red” (BRR).
As the cards are dealt, if three successive cards turn up in one of these sequences,
the player who claimed it gets to collect those three cards as a trick, and the dealing continues.
When all 52 cards have been dealt, the player who has collected the most tricks wins
(In a typical game, 7 to 9 tricks are won.)
"""
def __init__(self) -> None:
""" Generate a deck of cards containing blacks (26) and reds (26) """
self.all_cards = ['black' for _ in range(26)] + ['red' for _ in range(26)]
- Create a card selection: with and without winning strategy
def _card_selection(self) -> List[str]:
""" Select patterns of cards (n=3)
return ['black', 'black', 'red']
"""
return [random.choice(self.all_cards) for _ in range(3)]
def _card_selection_winning(self, reference_sequence: List[str]) -> List[str]:
""" Apply a winning method
Take a middle value, conjugate, put it in fromt of the sequence, and ditch the last value
Ex.1) BBR -> RBBR -> RBB
Ex.2) RRR -> BRRR -> BRR
"""
if not isinstance(reference_sequence, list) or len(reference_sequence) not in [3]:
return []
converted_value = 'red' if reference_sequence[1] in ['black'] else 'black'
winning_sequence = reference_sequence[:2]
winning_sequence.insert(0, converted_value)
return winning_sequence
- Create a core gameplay
def _play(self, is_winning_method_used: bool = False) -> Dict[str: bool]:
""" Play the game """
deck = self.all_cards.copy() # Get a dek of cards
random.shuffle(deck) # Shuffle a deck (in place)
# Select patterns
computer_sequence = self._card_selection()
player_sequence = self._card_selection_winning(computer_sequence) \
if is_winning_method_used else self._card_selection()
# Start playing game
current_game_sequence = []
final_result = {}
while deck:
drawn_card = deck.pop()
current_game_sequence.append(drawn_card)
# Adjust current_game_sequence to contain only three elements
if len(current_game_sequence) > 3:
current_game_sequence = current_game_sequence[-3:]
# Check the result
if len(current_game_sequence) == 3:
game_result = self._check_result(computer_sequence, player_sequence, current_game_sequence)
if True in game_result.values():
final_result = game_result.copy()
break
return final_result
- Create a result checking method
def _check_result(self, computer_sequence: List[str],
player_sequence: List[str],
current_game_sequence: List[str]) -> Dict[str, bool]:
""" Check the result of a game
All sequences must contain the same length of elements
return the result of a player winnig a game or not
"""
result = {
'computer_has_won': False,
'player_has_won': False
}
if computer_sequence == current_game_sequence:
result['computer_has_won'] = True
if player_sequence == current_game_sequence:
result['player_has_won'] = True
return result
- In order to make it easier for the experiment, I also wrote a method to run the game n times.
def start_experiment(self, is_winning_method_used: bool = False, n: int = 1000) -> Dict[str, int]:
""" Start an experiment and Display the result """
experimental_result = {'player_won': 0, 'computer_won': 0}
if not isinstance(n, int):
return None
for _ in range(n):
game_result = self._play(is_winning_method_used)
experimental_result['player_won'] += game_result['player_has_won']
experimental_result['computer_won'] += game_result['computer_has_won']
return experimental_result
- Lastly, putting them all together, we got a complete core game engine to be used for the experiment.
# Import libraries
import random
from typing import List, Dict, Any
# Core Game Engine
class GameEngine:
""" Two players play the game using an ordinary deck of cards.
The cards will be dealt out in a row, one after another.
Before the dealing begins, each player claims an ordered sequence of colors that might turn up,
for example “red black red” (RBR) or “black red red” (BRR).
As the cards are dealt, if three successive cards turn up in one of these sequences,
the player who claimed it gets to collect those three cards as a trick, and the dealing continues.
When all 52 cards have been dealt, the player who has collected the most tricks wins
(In a typical game, 7 to 9 tricks are won.)
"""
def __init__(self) -> None:
""" Generate a deck of cards containing blacks (26) and reds (26) """
self.all_cards = ['black' for _ in range(26)] + ['red' for _ in range(26)]
def _card_selection(self) -> List[str]:
""" Select patterns of cards (n=3)
return ['black', 'black', 'red']
"""
return [random.choice(self.all_cards) for _ in range(3)]
def _card_selection_winning(self, reference_sequence: List[str]) -> List[str]:
""" Apply a winning method
Take a middle value, conjugate, put it in fromt of the sequence, and ditch the last value
Ex.1) BBR -> RBBR -> RBB
Ex.2) RRR -> BRRR -> BRR
"""
if not isinstance(reference_sequence, list) or len(reference_sequence) not in [3]:
return []
converted_value = 'red' if reference_sequence[1] in ['black'] else 'black'
winning_sequence = reference_sequence[:2]
winning_sequence.insert(0, converted_value)
return winning_sequence
def _check_result(self, computer_sequence: List[str],
player_sequence: List[str],
current_game_sequence: List[str]) -> Dict[str, bool]:
""" Check the result of a game
All sequences must contain the same length of elements
return the result of a player winnig a game or not
"""
result = {
'computer_has_won': False,
'player_has_won': False
}
if computer_sequence == current_game_sequence:
result['computer_has_won'] = True
if player_sequence == current_game_sequence:
result['player_has_won'] = True
return result
def _play(self, is_winning_method_used: bool = False) -> Dict[str: bool]:
""" Play the game """
deck = self.all_cards.copy() # Get a dek of cards
random.shuffle(deck) # Shuffle a deck (in place)
# Select patterns
computer_sequence = self._card_selection()
player_sequence = self._card_selection_winning(computer_sequence) \
if is_winning_method_used else self._card_selection()
# Start playing game
current_game_sequence = []
final_result = {}
while deck:
drawn_card = deck.pop()
current_game_sequence.append(drawn_card)
# Adjust current_game_sequence to contain only three elements
if len(current_game_sequence) > 3:
current_game_sequence = current_game_sequence[-3:]
# Check the result
if len(current_game_sequence) == 3:
game_result = self._check_result(computer_sequence, player_sequence, current_game_sequence)
if True in game_result.values():
final_result = game_result.copy()
break
return final_result
def start_experiment(self, is_winning_method_used: bool = False, n: int = 1000) -> Dict[str, int]:
""" Start an experiment and Display the result """
experimental_result = {'player_won': 0, 'computer_won': 0}
if not isinstance(n, int):
return None
for _ in range(n):
game_result = self._play(is_winning_method_used)
experimental_result['player_won'] += game_result['player_has_won']
experimental_result['computer_won'] += game_result['computer_has_won']
return experimental_result
As can be seen from the method start_experiment, the default value of n is 1000 which means the game will be played 1000 times. To start the experiment, I wrote the main function as follows:
# Import libraries
import pandas as pd
import matplotlib.pyplot as plt
from game_engine import GameEngine
# Load Core GameEngine
game_engine = GameEngine()
# Main function
def main() -> None:
# Without a winning method
without_winning_method_res = game_engine.start_experiment(is_winning_method_used=False)
# With a winning method
with_winning_method_res = game_engine.start_experiment(is_winning_method_used=True)
# Prepare DataFrame
df_without_winning_method = pd.DataFrame([without_winning_method_res])
df_without_winning_method['cat'] = 'without'
df_with_winning_method_res = pd.DataFrame([with_winning_method_res])
df_with_winning_method_res['cat'] = 'with'
df_final = pd.concat([df_without_winning_method, df_with_winning_method_res])
df_final = df_final.set_index('cat')
print(df_final)
# Visualisation
df_final.plot.bar()
plt.show()
return None
# Execute the script
if __name__ == '__main__':
main()
Results
The results showed that playing with the winning strategy, Player(B) had a greater chance of winning (72.9%) against Player(A) from 1000 games played. On the other hand, playing without the winning strategy both players had a similar chance of winning 50-50.
NOTE: In this case, Player(A) is represented by computer
player_won computer_won
cat
without 555 575
with 729 271

Summary
The game that seems like a perfectly-balanced one may not be as it presents. A significant advantage can always be gained with the right strategies. As can be seen earlier that with a good mathematic strategy, one player could win more than 70% of the time.
Furthermore, with a combination of probability and computer programming, everything can be proved. Therefore, this stresses that technical skills are highly needed and can lead to new exploratory opportunities.